Rectangular White Ceramic Trough Drop In Sink
Scarabeo 5133
Highlights
Overview
Description
Looking for a trough sink? This rectangular drop in sink is a perfect choice for your bathroom. With a long 40 inch basin, this sink can used as a long single basin or a double basin sink with two spouts. This white ceramic sink features an overflow and has the dimensions of 39.4" x 14.2". Drop this self rimming sink into your counter space for a perfect modern look. This sink is made and designed in Italy by luxury sink designer Scarabeo and part of the Teorema 2 collection.
Product Details
- Rectangular white ceramic sink
- Trough style sink
- Drop in application
- With overflow
- No hole configuration
- From the Scarabeo Teorema 2.0 collection
- Standard drain size
Certifications & Listings
- IAPMO Certified
- US Standards Approved
- Massachusetts Plumbing Code Approved
- Uniform Plumbing Code (UPC/cUPC)
- National Plumbing Code of Canada
- ASME A112.19.2-2018/CSA B45.1-18
Technical Specifications
| Download: | |
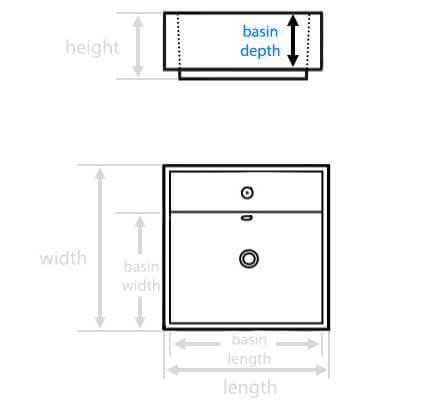
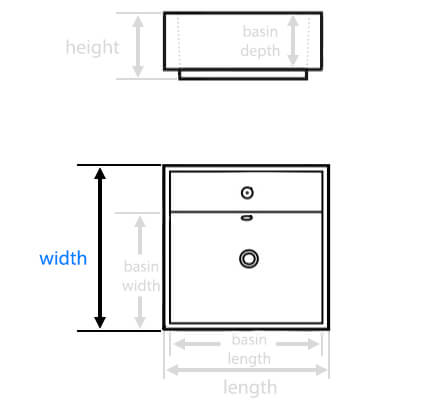
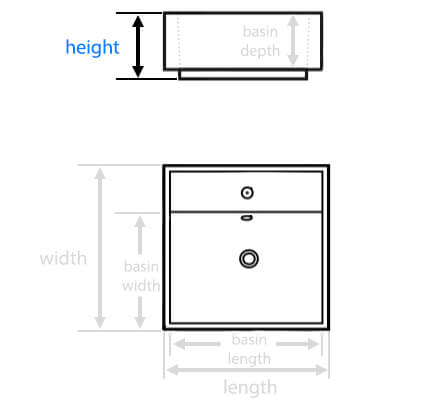
| Basin Depth: |
 4.7 Inches
|
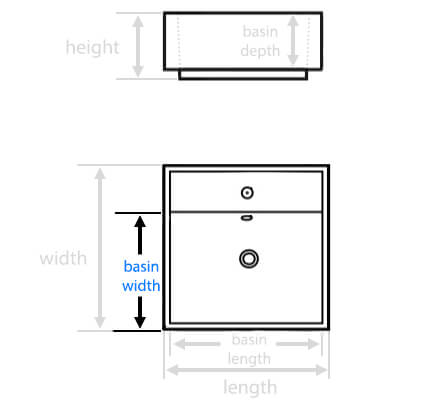
| Basin Width: |
14.1 Inches
|
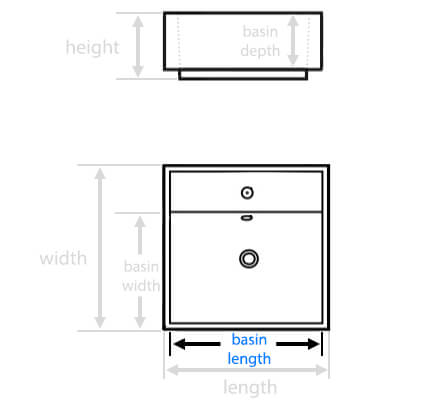
| Basin Length: |
39.3 Inches
|
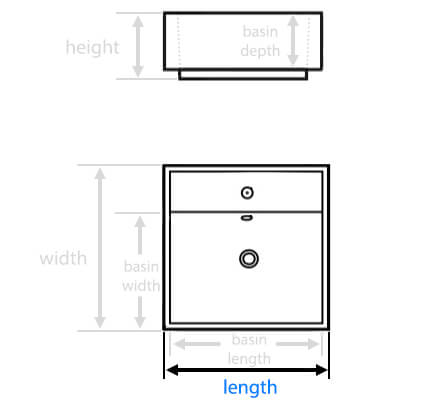
| Overall Length: |
39.4 Inches
|
| Overall Width: |
14.2 Inches
|
| Overall Height: |
6.69 Inches
|
| Weight: |
45 Lbs
|
Features
| Material: |
Ceramic
|
| Color: |
White
|
| Style: |
Modern, Contemporary
|
| Installation: |
Drop In
|
| Features: |
Has Overflow
|
| Faucet Holes: |
No Hole
|
| Shape: |
Rectangular
|
| Type: |
Trough
|
| Drain Hole Size: |
Standard, 1.75 Inch
|
| Faucet Hole Size: |
Standard, 1.38 Inch
|
| Compatible Drain SKU: |
S2077
|
| Compatible P-Trap SKU: |
HT32
|
| Faucet Included: |
No
|
| Angle Valves Included: |
No
|
| P-trap Included: |
No
|
| Pop-up Drain Included: |
No
|
| Overflow Hole: |
Yes
|
More Information
| Product Name: | Rectangular White Ceramic Trough Drop In Sink |
| SKU: | Scarabeo 5133 |
| Type: | |
| Collection Name: | |
| Brand Name: | |
| Country of Origin: | Italy |
| Categories: | |
| California Prop 65: |
Yes
|
Availability & Shipping
| Availability: | In Stock. |
| Shipping Method: | Ships with FedEx. |
Customer Photos
6 photos
Customer Reviews
13 reviews
| Wow! Is what this sink's statement is in my master bath remodel. The goal was quality, design and functionality. It's perfect! |
|
Tara on Nov 14, 2022
|
|
VERIFIED BUYER
|
| The sink arrived on time and was packed extremely well. It looks as advertised, measurements were accurate. The project has not started yet, so how it holds up and works is unknown. The drain and trap are the same. Well packed, seems well constructed and the finish is beautiful. |
|
Carlane on Jul 17, 2019
|
|
VERIFIED BUYER
|
| The sink is beautiful. Came well packaged and in great condition. I cannot wait to have it installed. |
|
Beverly Ann on Jun 5, 2020
|
| I have not installed or used this sink yet, but the packaging alone is worth 5-stars. Very well packaged and a beautiful product |
|
Joanna on Apr 11, 2023
|
|
VERIFIED BUYER
|
| Great sink! Love the product however the quality of the edges could be improved. The long edge on our product was visibly not straight but curved. |
|
Edward on Jul 2, 2021
|
|
VERIFIED BUYER
|
Product Q/A's
4 questions
?
I am ordering for a client. They love it in the photos. Can it be returned if they don?t live it in person being that they can?t view it before purchasing?A
The item is returnable as long as it meets timeframe and condition requirements. Full details on our return policy can be found here: https://www.thebathoutlet.com/company/return-policy.?
What is the height of the sink as measured from the countertop?A
Once installed, the countertop to the top of the sink is 2".?
What is the cut out measurements for this to sit flat as it appears in the photo?A
The cutout dimensions for this sink is roughly 37.8" L x 12.6" W -- however, we do not recommend performing any cutouts until the sink has been received for exact dimensions, as each sink slightly alters during the kilning process.
Do you have a question about this product?
Scarabeo Brand Information
Scarabeo's elegant, functional washbasins in many different models, have been stealing the scene in the bathroom since 1974.
The commitment and seriousness the firm has always shown, together with the quality of its products, have enabled it to make a name for itself on domestic and foreign markets and to set up successful collaboration agreements with the world's leading sanitary fixture manufacturers.
The other points of strength which always characterised the firm are its costant development of new ideals and ability to evolve in line with changing market demands. It is precisely this on-going evolution that brought the idea to present, in the last few years, the new ranges of vanity units which now form an extensive range that is being added to all the time.
Scarabeo's philosophy is to make the washbasin the focal point of the bathroom, and to make every effort to come up with new ranges and models for an increasingly demanding market, and to concentrate more on the quality and uniqueness of the products than on large quantities.
Customers Also Viewed
Related Searches
